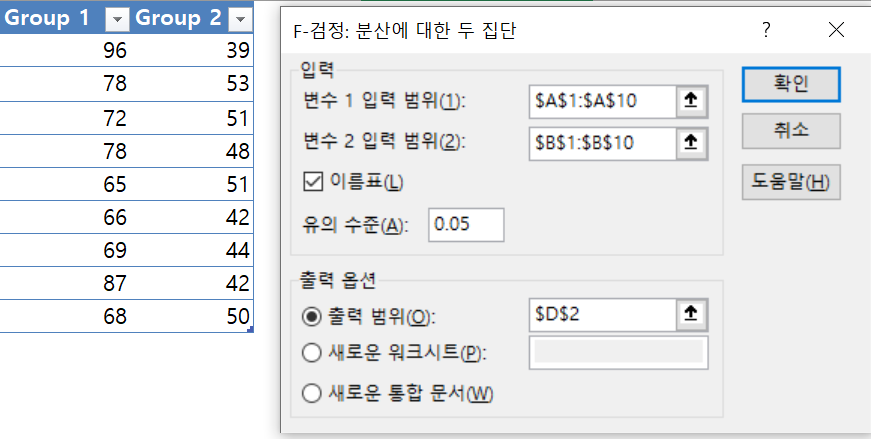
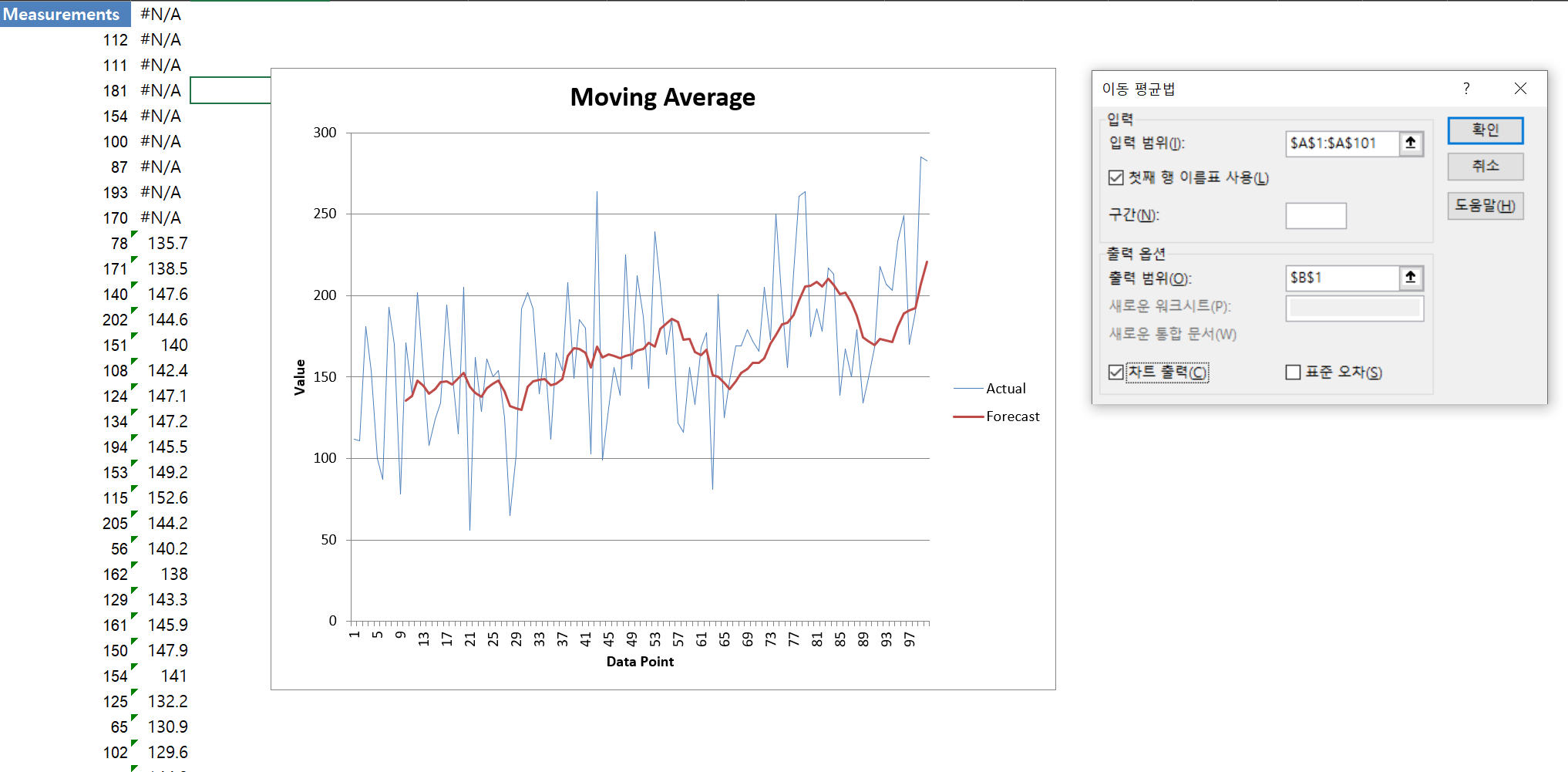
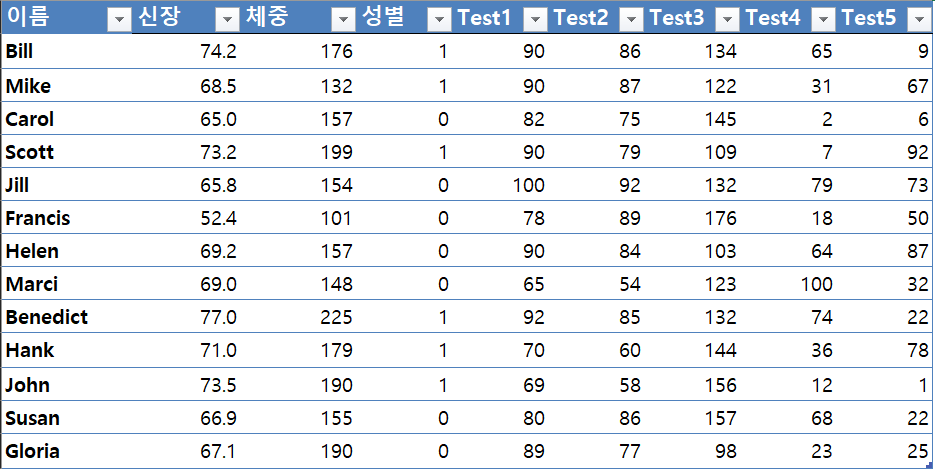
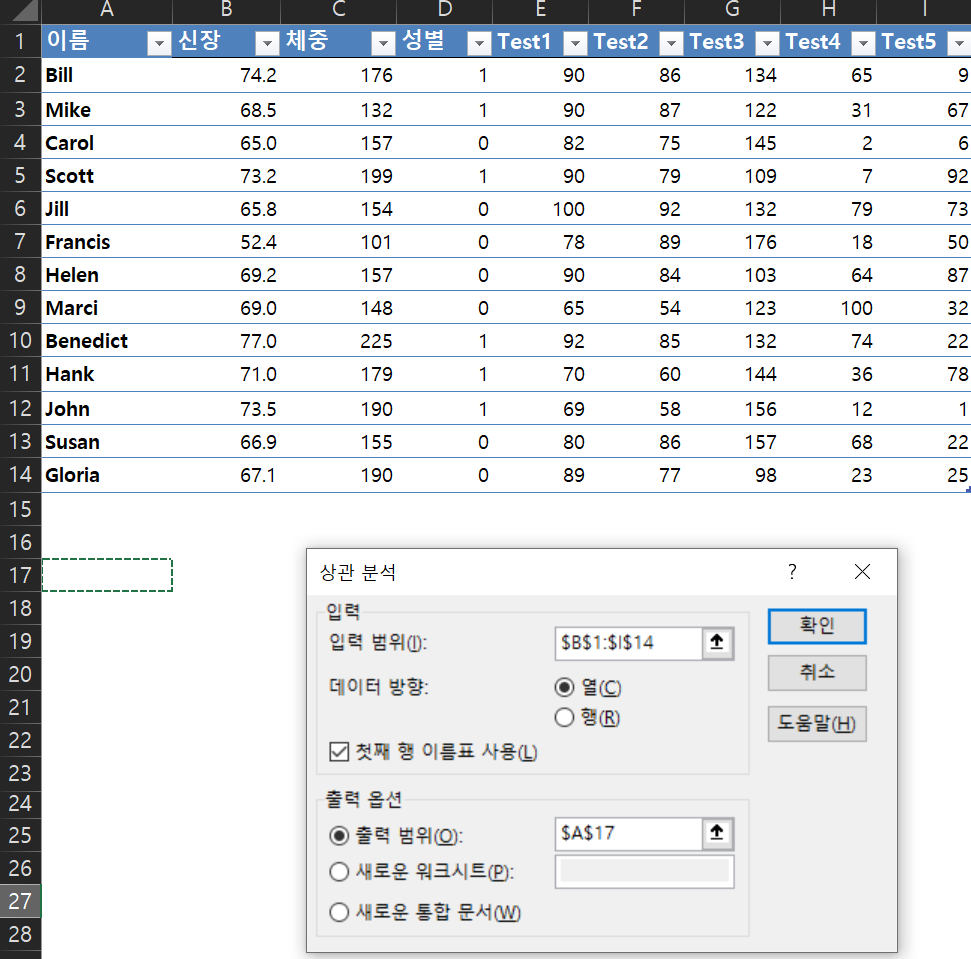
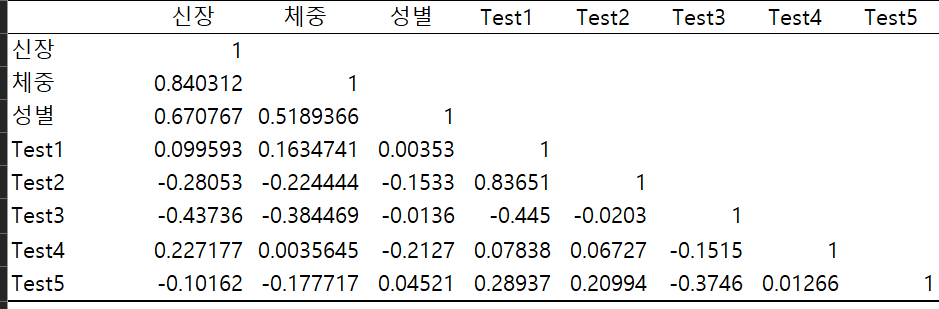
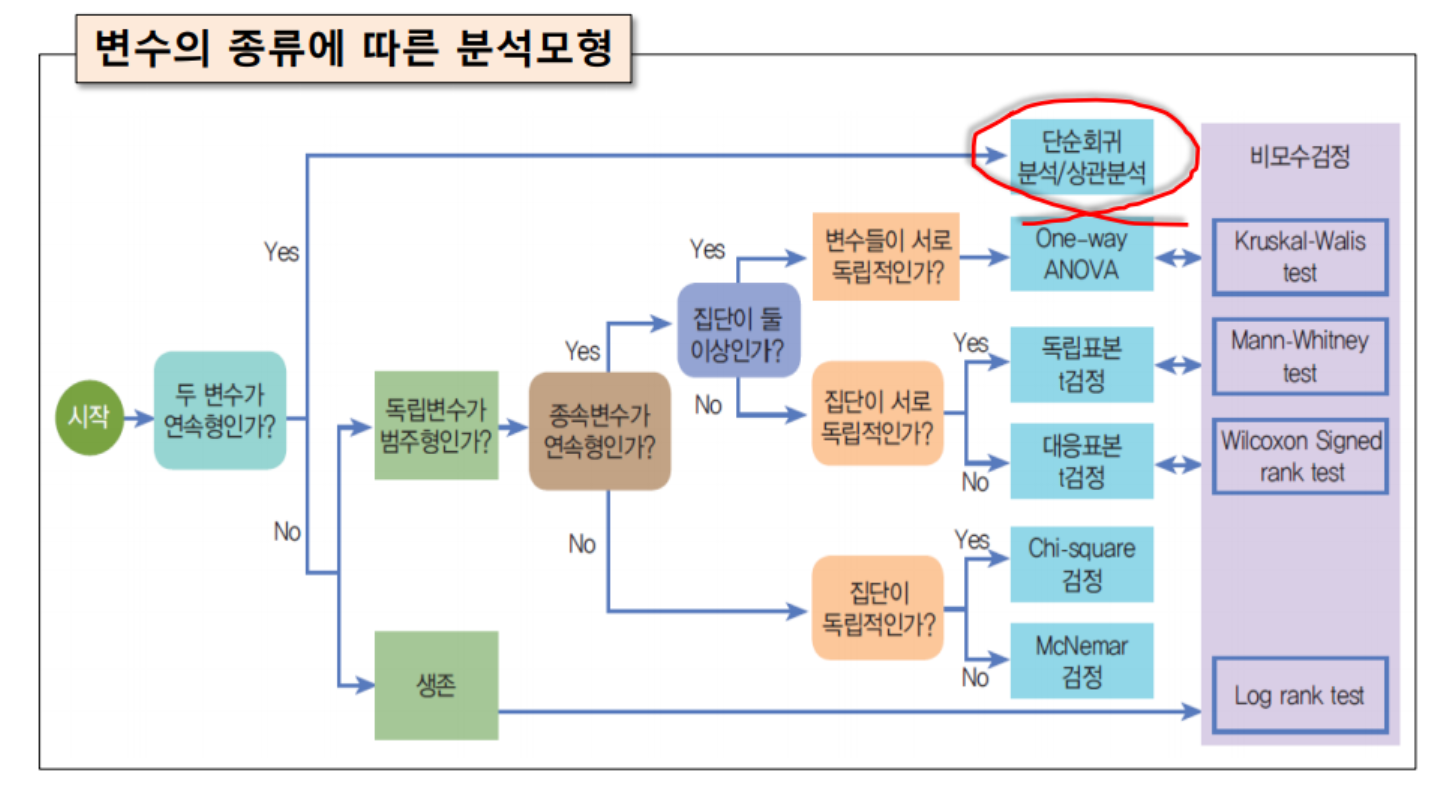
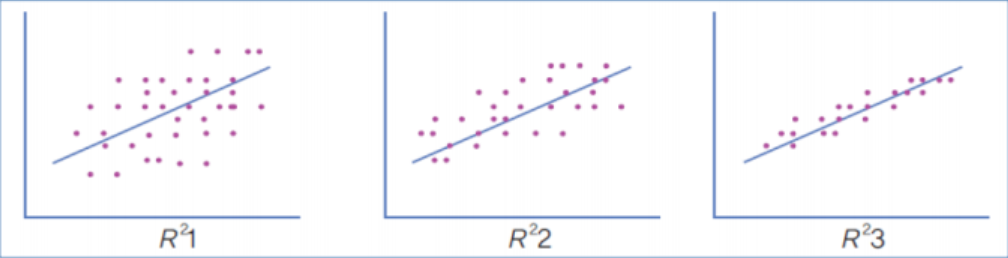
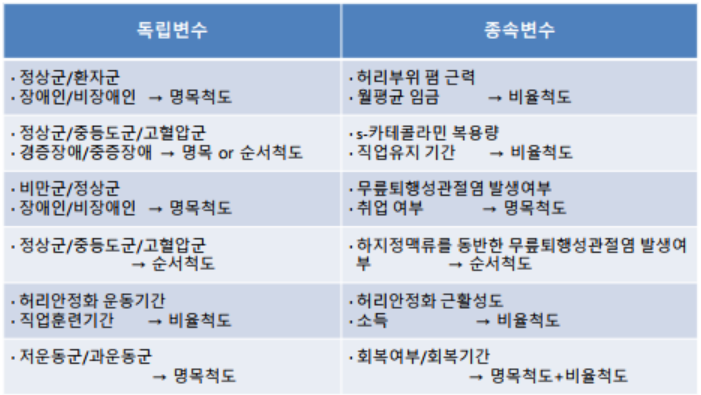
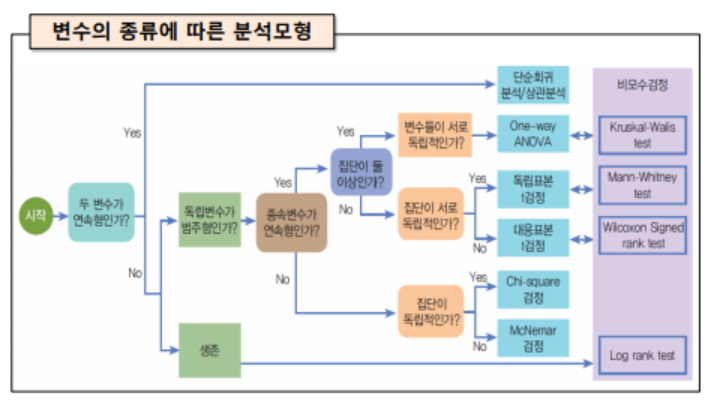
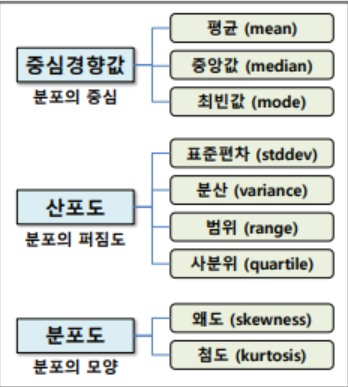
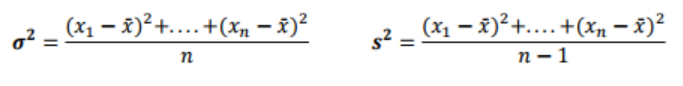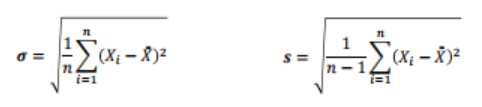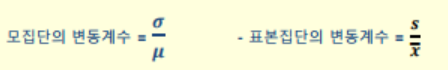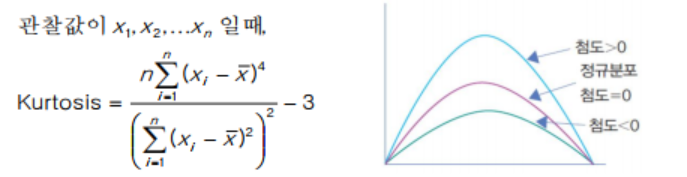주어진 신장 데이터의 기술통계를 구하시오

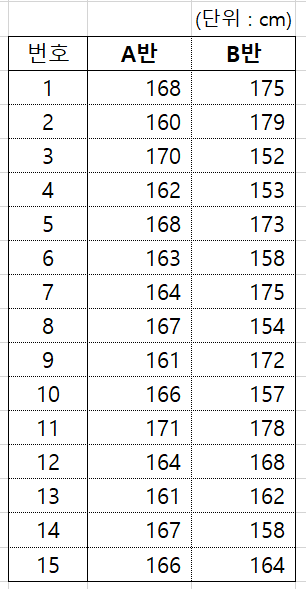
분석도구를 활용한 방법

• 분석도구 설정
  1. '파일’탭
  2. 좌측 하단 ‘옵션’
  3. 좌측 하단 ‘추가기능’
  4. 화면 중앙에 ‘분석도구’ 선택
  5. 중앙 하단 ‘이동;’ 클릭
  6. 추가 기능 창 생성
  7. ‘분석도구’ 체크
  8. 확인
  9. ‘데이터’ 탭에 ‘분석’ 메뉴에 ‘데이터분석’ 확인
• 기술통계법
  
  
  

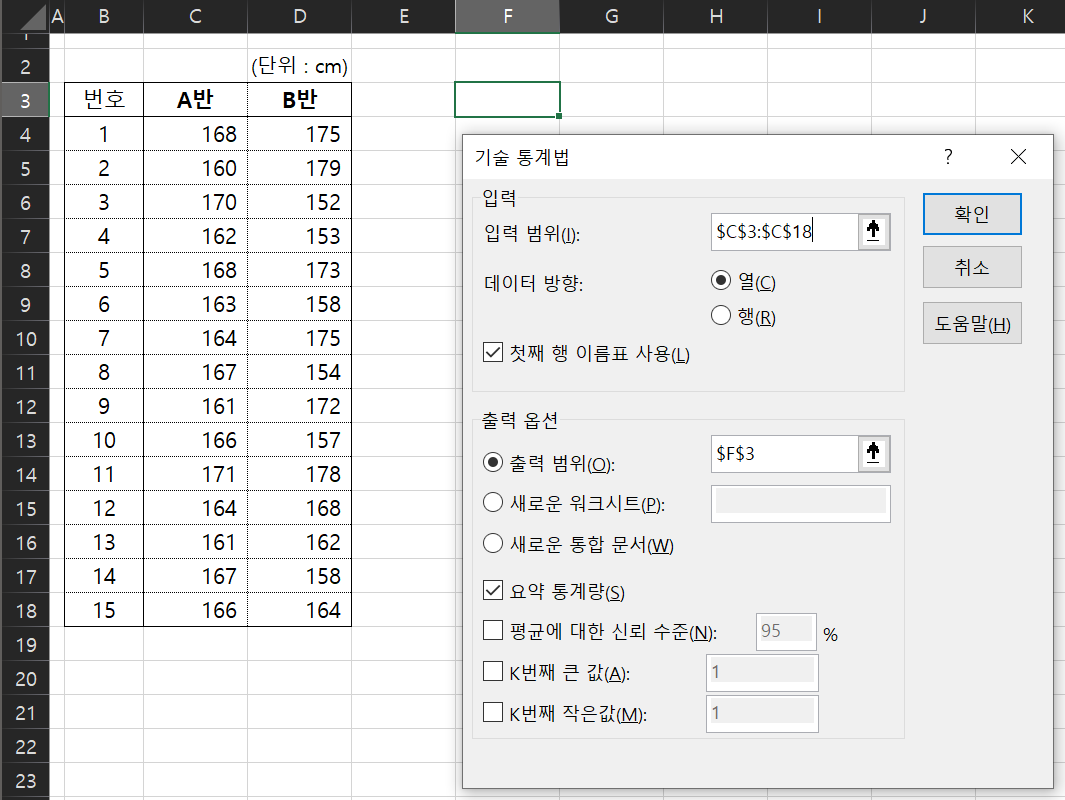
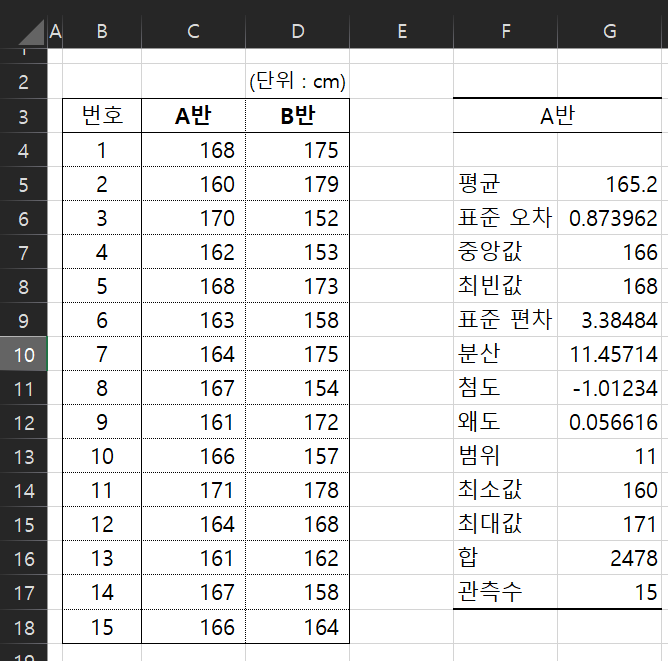
함수를 사용한 방법

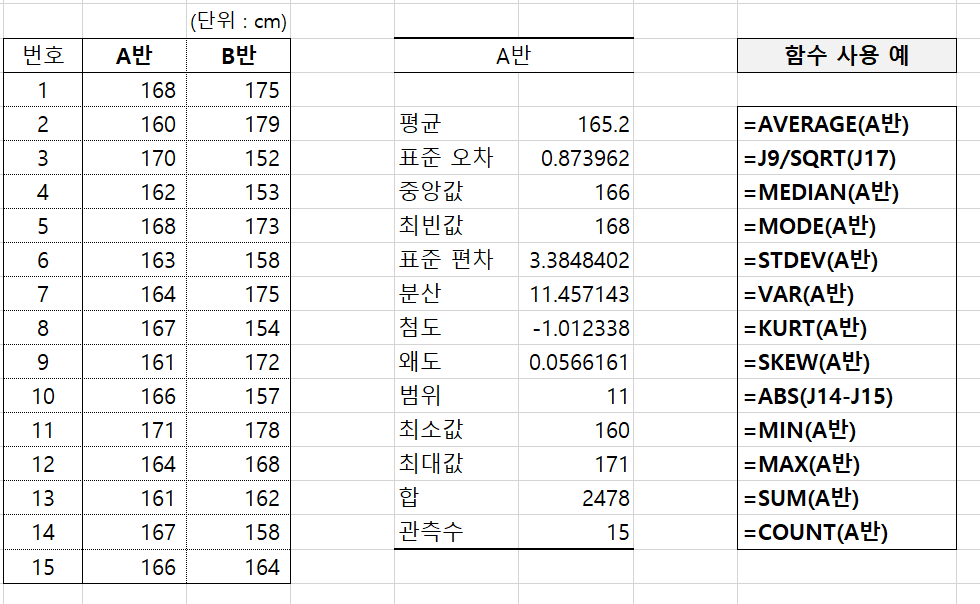
• 평균 AVERAGE()
• 표준오차 Val / SQRT()
• 중앙값 MEDIAN()
• 최빈값 MODE()
• 표준편차 STDEV()
• 분산 VAR()
• 범위 ABS()
• 최소값 MIN()
• 최대값 MAX()
• 합 SUM()
• 관측수 COUNT()

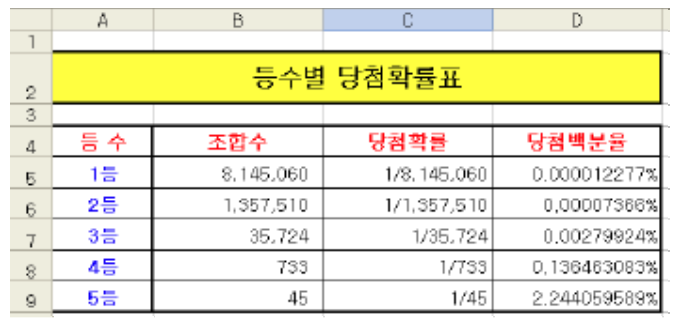
로또 6/45의 1~5등 까지의 조합수와 당첨확률을 구하시오

• 45개의 로또 공 가운데 무작위로 6개를 뽑는다
• 6개의 공을 무작위로 하나씩 뽑기 때문에 순서는 고려하지 않아도됨
• 해결방법
  1등 : 모두 당첨 -> 45개 공에서 순서 상관없이 6개가 한 번에
  = COMBIN(45,6) = PERMUT(45,6) / FACT(6)
  2등 : 5개 당첨 -> 6개 중에서 5개가 맞고 나머지 1개는 보너스 번호
  = COMBIN(45,6) / COMBIN(6,5) _ COMBIN(1,1)
  3등 : 5개 당첨 -> 6개 중에서 5개가 맞고 보너스 1개를 제외한 38개 중에 1개가 포함
  = COMBIN(45,6) / (COMBIN(6,5) _ COMBIN(39,1))
  4등 : 6개 중 4개 포함하고 39개 중에 2개 포함
  = COMBIN(45,6) / (COMBIN(6,4) _ COMBIN(39,2))
  5등 : 6개 중 3개 포함하고 39개 중에 3개 포함
  = COMBIN(45,6) / (COMBIN(6,3) _ COMBIN(39,3))
• 결과
  

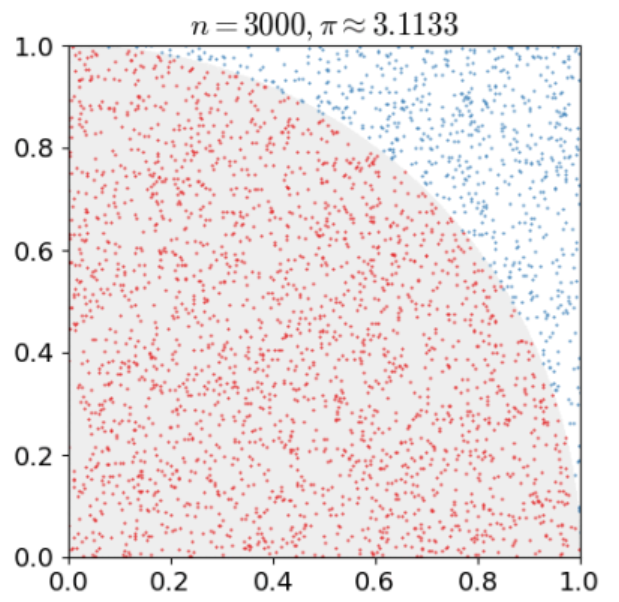
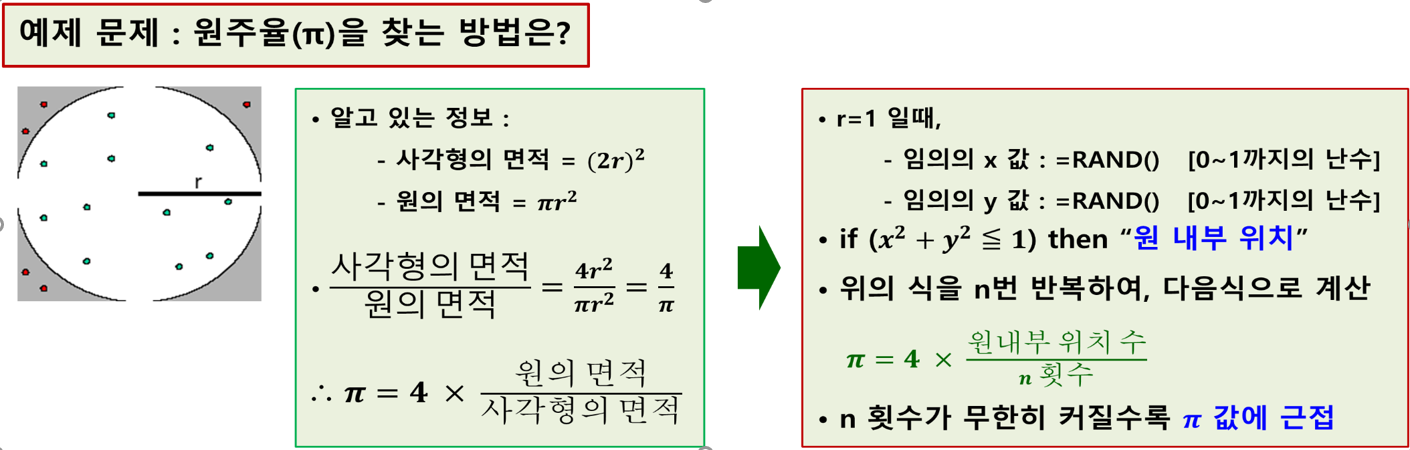
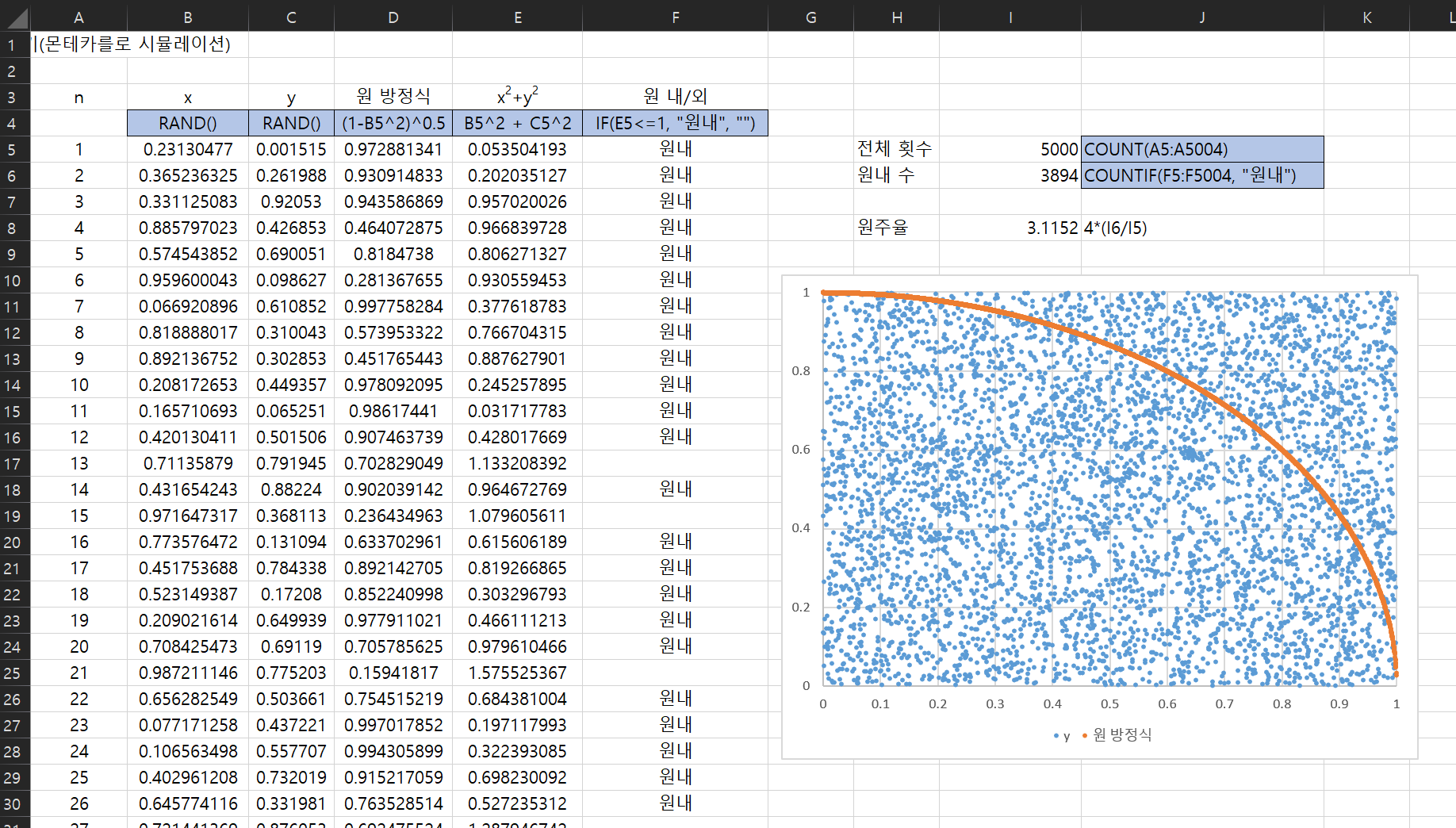
몬테카를로 시뮬레이션을 사용하여 원주율을 구하시오

• 알고 있는 정보
  1. 사각형의 면적 : (2r)^2
  2. 원의 면적 : πr^2
• 사각형의 면적/원의 면적 = 4r^2 / πr^2 = 4/π
• π = 4 * 원의 면적 / 사각형의 면적
• 랜덤으로 출력할 x, y
  = RAND() : 0~1까지의 난수
• 원의 방정식
  x^2 + y^2 = 1 이므로 y = (1-x²⁾0.5
  위 값이 원 내에 있는지 즉 1보다 작은지 확인 IF(Val<=1.“원내”,“원밖”)
• 원내 수 세기
  COUNTIF(범위, “원내”)
  

한 중학생의 시험점수를 이용하여 등수를 구하시오(전체성적평균과 표준편차는 제공)

문) 우리집 막내A 는 중학교 2학년에 재학중이다. 이번 중간고사 시험결과가 학교로부터 우편으로 배달되었다. 시험결과 안내는 A의 등수가 아니라 표로 제시되었다. 2학년 전체의 시험성적이 정규분포를 나타낼때 A의 등수는?

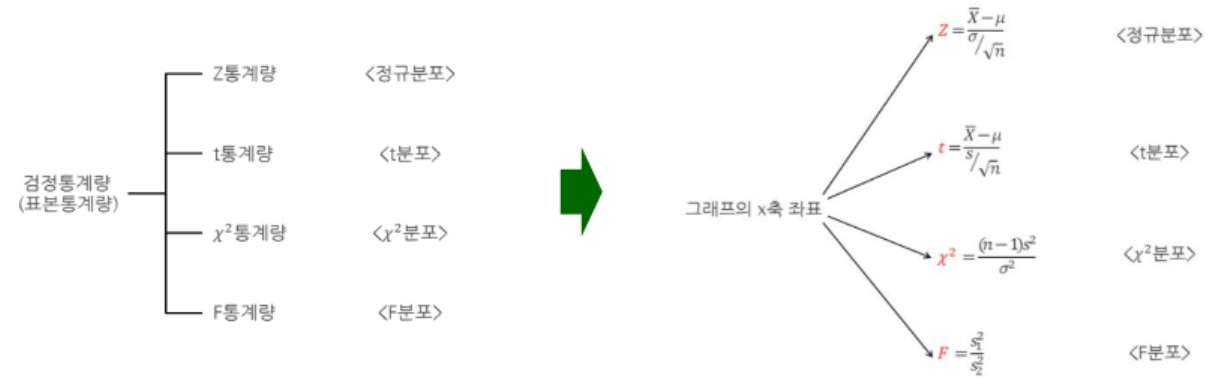
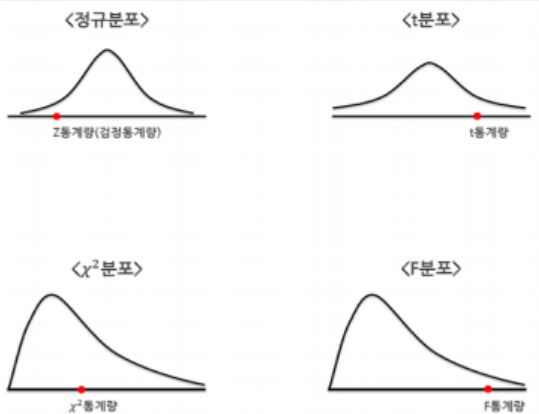
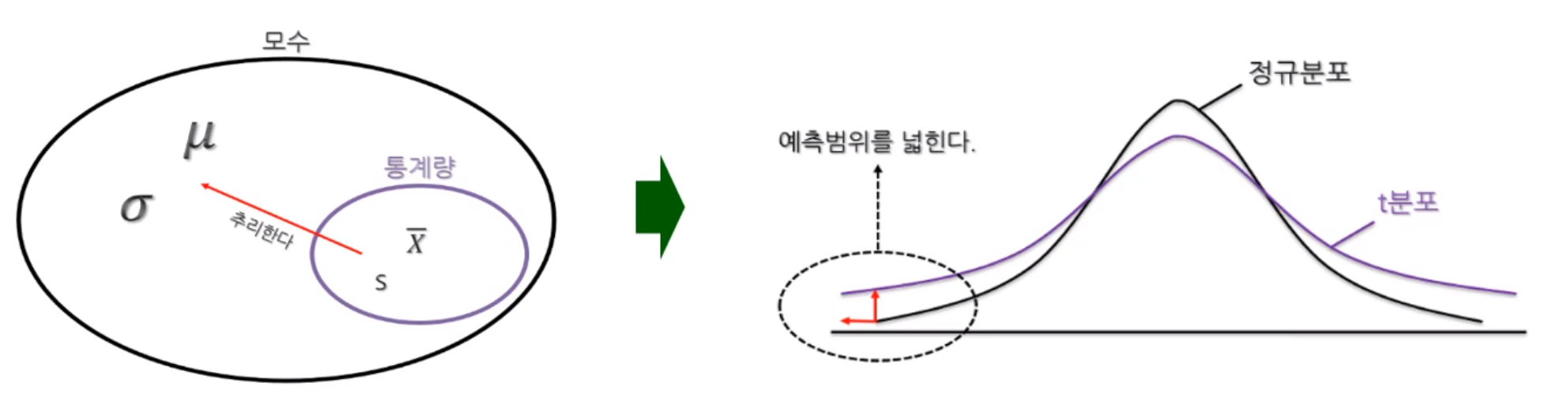
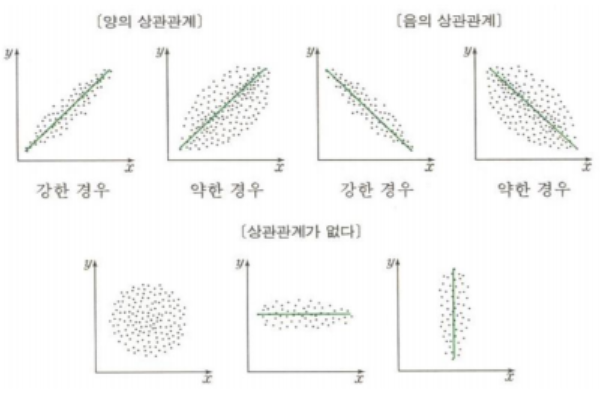
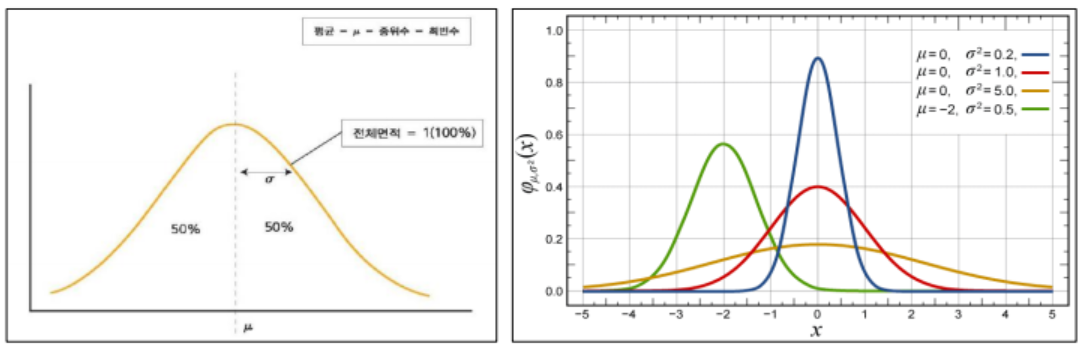
• 정규분포를 알고 가야한다.
  
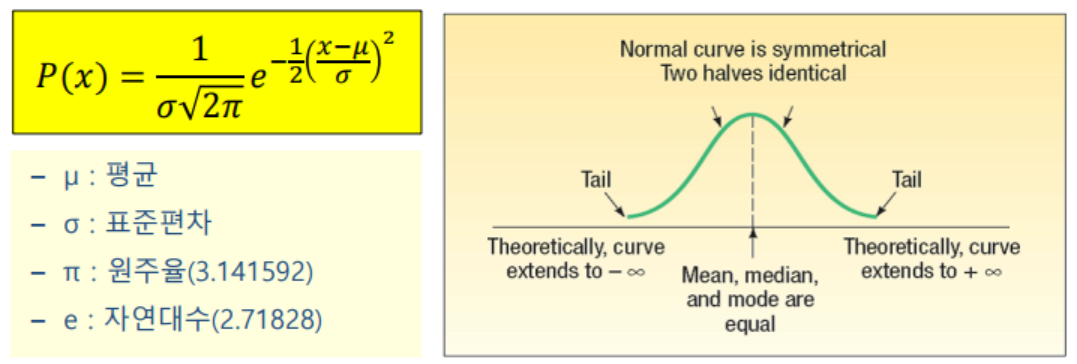
• 표준정규분포는 정규분포에서 평균이 0 표준편차가 1인 조건이 추가된다
  
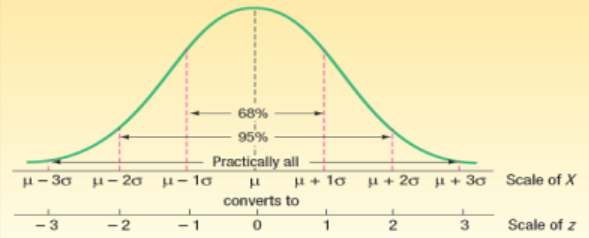
  평균에 가장 많은 수가 몰려있고 평균을 기점으로 좌우 대칭이고 서서히 분포가 낮아지는 종모양이다.
• z값을 구하자
  점수에서 평균을 빼고 그것을 표준 편차로 나누면 z이다
  z = (81.5 - 78.6) / 16.4 = 0.1768
• z에 대응하는 값을 정규분포표에서 찾기
  
  음수라면 절대값을 취한다
  0.1768이므로 반올림해서 0.18로 하겠다
  대응값 : 0.0714 를 찾았다
• 등수구하기
  대응값(면적)을 평균이 아닌 오른쪽 면적으로 바꾸어주고 전체 인원만큼 곱해야한다
  z가 양수라면 0.5-(대응값)
  z가 음수라면 대응값+0.5
  0.18은 양수이므로 0.5 - 0714 = 0.4286
  0.4286에 전체 학생수를 곱한다
  0.43 * 347 = 148.724
  149등이 추정 등수이다.
  참고링크

몬테카를로 방법

• 몬테카를로 카지노에서 따온 이름
• 무작위 추출된 난수를 이용하여 함수의 값을 계산하는 통계학의 방법
• 어느정도 오차는 존재
• 인공지능에서 많이쓰임
  • 바둑 AI
  • 체스 딥블루

몬테카를로 시뮬레이션

• 불확실성을 갖는 정보로 결론을 내리기 어려운 경우, 컴퓨터의 장점인 난수를 반복적으로 생성 적용시켜 근사적으로 답을 찾아내는 방법
  • EX) 원주율을 찾는 방법
• 어떤 문제에 대해 해를 무수히 많은 시도를 통해 얻어진 확률을 기반으로 하는 계산법

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import random

n = 1000000
count = 0

for i in range(n):
    # x,y를 무작위로 0~1 사이의 값으로 결정
    x = random.uniform(0,1)
    y = random.uniform(0,1)

    # 사분원 내부에 발생하는 경우수
    if (x**2 + y**2) <= 1 : count += 1

# 백만번 시도 중 사분원 내부일 경우에 대한 확률
# 사분원의 넓이이므로 일르 4배 곱하여 n 계산
print('phi', 4*count/n)

엑셀에서 만들어 보기

t검정

• 데이터분석 -> t-검정:쌍제비교
  
  -결과
  
• 해석
  • P가 0.05 이상인지 아닌지로 분석법을 채택할지 안할지 선택할 수 있음

F검정

• 데이터분석 -> F-검정:분산에 대한 두 집단
  
  -결과
  
• 해석
  • P가 0.05 이상인지 아닌지로 분석법을 채택할지 안할지 선택할 수 있음

이동평균법

• 데이터분석 -> 이동 평균법
  

통계 분석의 활용

회귀분석의 가설 Hypothesis

• 회귀방적식을 구한 후 검증이 필요
• 단순회귀직선의 적합도 검증
  • 가설의 설정 : Y = a + bx + c
  • 귀무가설 : b = 0
  • 대립가설 : b != 0
  • 귀무가설은 통계학에서 처음부터 버릴 것으로 예상하는 가설
  • H분석
    • H0 : 독립변수 x가 y에 영향을 주지 않는다
    • H1 : 독립변수 x가 y에 영향을 준다
• 통계적 가설 검증은 F값으로 확인
  • 유의확률(p값) < 0.05 : 이 모형이 적합 -> 귀무가설 채택
  • 유의확률(p값) > 0.05 : 이 모형은 부적합 -> 귀무가설 기각
  • 유의확률이 0.05는 오류가 나올 확률이 5%라는 의미로 유의수준이 95% 신뢰도를 갖는다를 의미
    • 그래프를 그렸을 때 양쪽으로 벗어날 확률임

요약 가설과 검정 방법

1. 정규성 검정(데이터 탐색)
   • H0 : 모집단 분포는 정규분포를 따른다
   • H1 : 모집단 분포는 정규분포를 따르지 않는다
2. 분산의 동질성 검정(독립 T검정, 분산분석)
   • H0 : 각 집단의 분산은 동질성을 가진다
   • H1 : 각 집단의 분산은 동질성을 가지지 않는다
3. 독립성 검정(상관분석)
   • 상관계수 : -1 <= r <= 1
   • H0 : 상관계수 e = a : 독립
   • H1 : 상관계수 e != 0 : 종속

• 유의확률이 0.05보다 크면 귀무가설이 채택된다

가설 검정

• 가설검정은 모집단의 모수가 이럴 것이다라를 가설을 위해 모수인 u, a^2, p를 사용해서 귀무가설과 대립가설 설정
  • 일반적으로 표본통계량으로 대체
  • 각 표본집단에 맞는 확률분포에 따라 신뢰구간 추정
  • 각 확률분포의 x 값을 검정통계량으로 사용

t분포; t-distribution

• 모집단의 특징을 분석하기에는 시간과 비용의 제약으로 일반적으로 표본조사를 실시하고, 이를 모집단과 같을 것임을 추정함
• 표본의 개수가 적으면(일반적으로 30개 미만) 신뢰도가 낮아짐
• 따라서 정규분포 보다 예측 범위가 넓은 분포인 t-분포를 사용
  

카이제곱 분포

• 명목 및 서열척도의 범주형 변수를 분석하기 위해 한 변수의 범주를 다른 변수의 범주에 따라 빈도를 교차분석하여 두 변수 간 독립성과 관련성을 분석
• 제곱된 값 분산을 다루기 때문에 음수값이 없고 양수만 존재 - 오른쪽 만 꼬리가 긴 비대칭 모양
  

F분포; F-distribution

• 집단의 분산을 추정하고 검정할 때 사용하는 분포
• 카이제곱 분포와 유사하나 한 집단의 분산을 파악하는 카이제곱과 달리 F분포는 두 집단의 분산을 비교
• 3개 이상 집단의 분산을 비교하는 것을 보통 분산분석:Analysis of Variance이라고 하며 신뢰구간 추정과 가설검증, 분산분석에 F-분포가 많이 사용됨
  

요인분석

• 일련의 관측된 변수에 근거하여 직접 관측할 수 없는 요인을 확인하는 분석 기법
  • 경제활동, 가계수입, 주택보급율, 출생률 등 수많은 변수를 사용해야 하나, 몇가지 적은 변수로 묶어 단순화하는 것
• 항목 간의 상관관계가 높은 것끼리 하나의 요인으로 묶거나 중요도가 낮은 변수는 제거
  • 하나의 요인으로 묶어진 항목들은 하나의 개념을 측정한 것으로 간주하며, 요인 내의 항목은 수렴적 타당성, 요인간에는 변별적 타당성이 적용된 것으로 해석
• 같은 개념을 측정하려고 하는 변수들이 동일한 요인으로 묶이는지 확인하고자 하는 경우
• 전제조건
  • 모든 변수가 드간척도 이상의 연속형 변수로 측정되어야 함
  • 각 변수는 서로 독립이며 정규분포, 등분산을 이루고 있어야 함
  • 표분의 수는 50이상 내지 변수의 5배수 이상을 권고하고 있음

분석도구 옵션

• 파일 -> 옵션 -> 추가기능 -> 관리: 이동클릭 -> 분석도구체크 -> 확인
• 데이터탭 -> 분석 메뉴 -> 데이터분석 확인

회귀분석

• 다음과 같이 Adv-홍보지출액, bp Diff-이자지급액, Deposits-새로운 예치금을 통해 회구분석을 해보자
  
• 회귀분석 선택
  
• 값 입력
  • Y는 원하는 목표
  • X는 무엇을 통해 Y를 예측하고 싶은지
    
• 결과
  
• 해석
  • 결정계수가 0.58이면 0.6에 가까우므로 Adv와 bp Diff가 Depositis에 영향이 있다고 할 수 있음

상관계수

• 다음과 같이 사람의 신장과 체중 성별 그리고 기타test끼리의 상관관계를 확인해보자
  
• 데이터분석의 상관분석 클릭
• 값 입력
  • 입력 범위시 이름은 의미가 없으므로 제외
  • 첫 행이 이름표가 있으므로 체크
    
• 결과
  
• 해석
  • 체중과 신장은 큰 상관관계까 있다
  • 성별은 신장과 체중과 연결관계가 있다
  • Test1과 신장, 체중, 성별은 큰 의미가 없다
  • 최대 1.0을 넘을 수 없음
  • 음수일 때는 전혀 상관없음으로 해석

통계 분석의 활용

기술통계화 추론통계

• 변수의 종류에 따라 분석하는 모형이 다르다
  

회귀분석 Regression Analysis

• 변수와 변수 사이의 관계를 통계적으로 분석하는 방법
• 독립변수 값에 의한 종속변수 값을 예측하기 위해 사용 - 단순회귀 분석 - 하나의 종속변수(Y)와 하나의 독립변수(X)간의 관계분석 - y = ax + b 형태 - 다중회귀 분석 - 하나의 종속변수(Y)와 둘 이상의 독립변수(X1, X2, …)간의 관계 분석 - y = ax1 + bx2 + c 형태
• 독립변수에 의한 종속변수 변화량을 근사한 방정식이기 때문에 기울기가 같더라도 측정값의 분포는 다를 수 있음
• 결정계수(R^2)로 나타냄
  

결정계수 R^2 ; coefficient of determination

• 추정한 선형 모형의 적합도를 나타내는 척도로 사용
• 즉 독립변수가 종속변수의 몇 %인가를 설명하는 수치
  • ex) 0.63이라면 63% 적합성을 갖음
  • 0이면 기울기는0이고 1이면 오차는 0
• 선형 회귀분석에서 '전체 제곱합 중에서 회귀 제곱합이 나타내는 비중’을 의미
  • 0 <= R^2=SSR/SST <= 1
  • SSR : 회귀 제곱합
  • SST : 총 제곱합
  • SSE : 잔차 제곱합
• 계산방법
  • 최소자승법에 의한 수학적으로 계싼
    • 측정갑과 임의의 수직 거리의 제곱의 총 합이 최소가 되는 방정식 도출
  • Excel에서 LINEST(Y,X) 함수 사용

F값의 이해

• F 값은 모형 적합도를 나태냄
• 0.05보다 작다면 적합
• 0.05보다 크면 부적합
• 즉 0.05 보다 커야 회귀식이 유의미함

SPSS에서 유의사항 (R 같은 것)

• 공선성 : 독립변수 간에 상관성이 높아 회귀분석에 적합하지 않음
• Cook의 통계량 값이 1.0 이상이면 이상점으로 간주
• 잔차의 등분산성, 독립성, 정규성 검증

상관계수 correlation coefficient

• 연속형 두 변수의 관련성의 세기 분석에 사용
• -1 <= r <= 1
• Pearson 상관계수
  • 모집단의 분포가 정규분포에 가까우면 사용
  • 두 변수가 양적자료인 경우 사용
• Spearman 상관계수
  • 모집단이 비정규분포를 나타낼 때 사용
  • 두 변수 중 하나라도 순위척도인 경우
    

언제사용할까?

• 선형회귀분석

  1. 아버지의 혈압과 아들의 혈압 관계
  2. 입원기간과 수술시간의 관계
  3. 혈압과 연령의 관계

• 로지스틱 회귀분석

  1. 경제적 수입과 삶의 질의 정도와의 관계
  2. 통증과 암의 진행단계와의 관계

• 회귀분석은 종속변수와 독립변수 모두 양적 변수이어야 함

• 종속변수가 질적이고 독립변수가 양적이면 로지스틱 회귀분석 사용

정규분포의 예시

정규분포 Normal Distribution

• 연속확률변수에 속하고 모분포, 가우스 분포라 하여 이상적인 모형
• 평균 : 모집단평균
• 분산 : <b선모집단분산
• 평균과 표준편차에 의해 정의되고 결정되는 대칭 곡선
  
• 평균 = 중앙값 = 최반값
• 분포의 곡선 면적은 1.00
• 평균에 대해서 대칭형태
• 확률 값은 중앙값에 양 극단으로 갈수록 0에 가까워짐(무한대)
• 평균값에 의해 결정되고, 분포는 표준편차에 의해 결정
  

표준정규분포 : z-분포

• 평균=0, 표준편차=1 인 정규분포를 표준정규분포라고 함
  
  
• 표준정규확률분포(z값)
  • 확률분포표는 양수 z의 값에 대해서 표준정규분포가 0~z사이에 있을 확률(면적)을 기록한 것
  • 음영표시 확률 (47.5%)는 z값 1.9와 0.06을 합쳐 1.96이며, 절대값 1.96 바깥에 있는 부분의 확률은 2*0.025=0.05 , 즉 5%
  • 이는 표준편차 1.96배 바깥의 범위의 확률이 5%라는 의미
    

중심극한정리 central limit theorem

• 정규분포를 이루는 모집단에서 추출한 표본집단의 평균과 표본분포는 정규분포를 갖음
• 모집단이 정규분포가 아니라도 표본의 크기가 증가함에 따라 모집단에 관계없이 표본집단 평균은 정규분포에 가까워지는데 이를 중심극한정리라 함
• 대상자가 30명 이상 일 때, 모집단에 상관없이 표본집단은 정규분포를 이룬다고 하고, 대상자수가 많을수록 정규성에 가까워짐

문제풀기 1

문) 전문뉴스 라디오채널 A방송 청취자의 평균 청취시간 분포가 정규분포를 따른다고 가정할 때, 이 분포의 평균은 15.0분, 표준편차는 3.5분이다.
각 구간별 청취시간을 나타낼 확률을 구하시오

1. 20분 이상
2. 20분 이하
3. 10분과 12분 사이
4. 25분 이상

• Tip : NORM.DIST(x,y,z, True) 활용

1. 20분 이상

1
2

=norm.dist(20, 15.0, 3.5, true)
/// 0.9234

20분 이상 청취할 확률은 1.0 - 0.9234 = 0.0766 -> 7.6%

문제풀기 2

문) 우리집 막내A 는 중학교 2학년에 재학중이다. 이번 중간고사 시험결과가 학교로부터 우편으로 배달되었다. 시험결과 안내는 A의 등수가 아니라 표로 제시되었다.

• 2학년 전체의 시험성적이 정규분포를 나타낼때 A의 등수는?

변수의 종류

척도에 따른 분류

• 척도 : 입력자료를 수치적으로 측정하는 단위
• 명목 척도 : 성별, 직업, 지역 -> 순서와 무관, 수학적 계산 불가
• 순서 척도 : 대소, 다과 등 서열적 자료 -> 순서상 상대적 위치 표현
• 등간 척도 : 온도, 만족도 -> 수학적 연산 가능
• 비율 척도 : 매출액, 가격 -> 절대적 원점 존재, 수학적 연산 가능
  

인과관계예 따른 분류

• 독립변수(설명변수)
  • 다른 변수에 영향을 주는 변수
  • 원인에 해당
• 종속변수(반응변수)
  • 다른 변수에 영향을 받는 변수
  • 결과에 해당
    

자료형식에 따른 분류

• 숫자변수
  • 숫자로 처리되는 변수
• 문자변수
  • 문자열로 처리되는 변수
• 날씨변수
  • 날짜 표기형식으로 처리되는 변수

기술통계와 추론통계

• 기술통계
  • 측정이나 실험으로 수집한 자료의 정리, 표현, 요약, 해석 등을 통해 자료의 특성과 변수 간의 관계를 분석하는 통계적 방법
  • 도수분포, 백분율, 평균, 표준편차 등 분석 포함
• 추론통계
  • 표본정보를 가지고 그 모집단의 특성 및 가능성 등을 추론해내는 통계적 방법
  • 표본통계량을 이용하여 모수를 추론
  • 추론과정에서 모집단의 분포가 정규분포이면 모수검정 실시
  • 모집단이 정규분포를 가정하지 못하면 비모수검정 실시
    

범주형 데이터 기초분석

• 빈도분석
  • 실행메뉴
    • 분석 -> 기술통계량 -> 빈도분석
  • 분석할 변수의 빈도, 퍼센트, 무응답을 제외한 유효퍼센트, 누적퍼센트 등이 분석
• 통계량
  • 수학적 분석결과 표시
  • 백분위수
  • 산포도
  • 중심경향
  • 분포
• 도표
  • 범주형 변수
    • 막대도표
    • 원도표
  • 정량적 변수
    • 히스토그램
    • steam&leaf
    • Box-plot

연속형 데이터 기초 분석

기술 통계값

• 주어진 데이터를 요약하며 의미 있는 몇 개의 값으로 분석
• 요약과정에서 정보의 손실에 의한 정확성이 상실되나, 대부분 요약성이 정확성보다 중요한 의미를 갖음
  

평균값 mean

• AVERAGE()
• 평균값은 어디에나 존재
• 자료의 모든 값을 고려
• 극단치에서 변동의 폭이 심함
  

중앙값 median

• MEDIAN()
• 중앙값은 어떤 경우에나 존재
• 자료의 모든 값 자체를 고려하지는 않고 몇 개의 값이 있는지만 고려
• 극단적인 자료에서도 크게 변하지 않음
• 극단치가 있다면, 평균값보다 중앙값이 더 대표성을 띔

최빈값 mode

• MODE()
• 특히 이름으로 표현한는 명목변수나 이산변수를 기술할 때 사용
• 하나 이상일 수 있지만, 전혀 없을 때도 있음
• 모든 값을 반영하지는 않음

범위 range

• MAX() - MIN()
• 연속형 변수에서 사용
• 변수의 최고값에서 최소값을 뺀 것
• 계산하기에 간편함
• 최고값과 최소값에 의해서 범위가 결정되므로 그 사이에 값들의 퍼진 정도는 알수 없음
• 극단치가 있을 때는 변동이 큼

분산 variance

• 모집단의 분산 VAR.P()
• 표본집단의 분산 VAR.S()
• 측정값의 편차를 제곱하여 계산
• 모 분산의 단위는 관측 값이 갖는 측정단위와 일치하지 않음
  

표준편차 standard eviation

• 모집단 표준편차 STDEV.P()
• 표본집단의 표준편차 STDEV.S()
• 분산의 양의 제곱근
• 측정값의 측정단위와 일치하기 위함
• 크다
  • 자료가 평균값을 중심으로 광범위하게 분포
• 작다
  • 평균값을 중심으로 밀접하게 분포
    

변동계수 coefficient of variation, CV%

• 변동계수는 표준편차를 평균으로 나눈 값
• 측정단위에 따라 표준편차의 값의 크기가 달라지므로, 단위가 다른 두 집단을 비교하는 경우, 두 표준편차의 단위를 같게 하기 위해 표준편차를 평균으로 나눈 값에 100을 곱하여 CV%로 표시(그전에는 단위가 없음)
  

사분위수범위 interquartile range : IQR

• 상위 25%에 해당하는 값과 하위 25%에 해당하는 값을 제외하고 범위를 구한 값
• IQR는 주우이수를 중심으로 상위25%와 하위 25% 관측값의 차이를 의미
  

왜도 skewness

• SKEW()
• 0SKEW.P()
• 분포도의 기울어진 방향과 정도를 나타내는 양
• '0’에 가까울수록 정규분포와 비슷
  
  

첨도 kurtosis

• KURT()
• 분포도의 모양이 얼마나 뾰족한 가를 나타내는 양
• '0’에 가까울수록 정규분포와 비슷
  
  

엑셀에서 통계도구 사용하기

• 파일 -> 옵션 -> 추가기능 -> 분석도구 -> 이동 -> 분석도구 check
• 데이터 탭 -> 데이터분석

python 자료형

• 저장 모델

  • Literal : 단일 종류
  • Container : 종류에 무관

• 변경 가능성

  • Immutable : 변경 불가
  • Mutable : 변경 가능

• 접근 방법

  • Direct : 직접 할당
  • Sequence : 순서 중시
  • Mapping : 순서 무관
  • Set : 중복 불가

• 튜플은 최초에 입력한 데이터 변경이 불가

• 리스트는 최초에 입력한 데이터 변경 가능

• 사전은 순서에는 상관 없지만 중복 가능

• 집합은 중복 불가능

C자료형

순열(Permutation)

-> PERMUT(number, number_chosen)

• 서로 다른 n개의 원소에서 r개를 중복없이 골라 순서에 상관 있게 나열하는 것으로 n개에서 r개를 택하는 순열이라고 함

$nPr = n * (n-1) * (n-2) * ... * (n - r + 1) = n! / (n-r)!$

• 순열의 종류

1. 순열
2. 중복순열 : n개에서 r개를 순서에 상관 있게 뽑는데 중복가능
3. 등차순열 : n에서 r개를 뽑는데, n개 중에서 똑같은 것이 섞인 경우
4. 원순열 : n개를 원형으로 나열하는 경우

조합(Combination)

-> COMBIN(number, number_chosen)

• 서로 다른 n개의 원소에서 순서에 상관없이 r개를 뽑을 때, 이때 n개에서 r개를 택하는 조합

$nCr = nPr / r! = n!/ (n-r)!r!$

• 조합의 종류

1. 조합
2. 중복조합 : n개에서 r개를 순서에 상관없이 뽑는데 중복을 허락하는 경우