
통계 분석의 활용
회귀분석의 가설 Hypothesis
- 회귀방적식을 구한 후 검증이 필요
- 단순회귀직선의 적합도 검증
- 가설의 설정 : Y = a + bx + c
- 귀무가설 : b = 0
- 대립가설 : b != 0
- 귀무가설은 통계학에서 처음부터 버릴 것으로 예상하는 가설
- H분석
- H0 : 독립변수 x가 y에 영향을 주지 않는다
- H1 : 독립변수 x가 y에 영향을 준다
- 통계적 가설 검증은 F값으로 확인
- 유의확률(p값) < 0.05 : 이 모형이 적합 -> 귀무가설 채택
- 유의확률(p값) > 0.05 : 이 모형은 부적합 -> 귀무가설 기각
- 유의확률이 0.05는 오류가 나올 확률이 5%라는 의미로 유의수준이 95% 신뢰도를 갖는다를 의미
- 그래프를 그렸을 때 양쪽으로 벗어날 확률임
요약 가설과 검정 방법
- 정규성 검정(데이터 탐색)
- H0 : 모집단 분포는 정규분포를 따른다
- H1 : 모집단 분포는 정규분포를 따르지 않는다
- 분산의 동질성 검정(독립 T검정, 분산분석)
- H0 : 각 집단의 분산은 동질성을 가진다
- H1 : 각 집단의 분산은 동질성을 가지지 않는다
- 독립성 검정(상관분석)
- 상관계수 : -1 <= r <= 1
- H0 : 상관계수 e = a : 독립
- H1 : 상관계수 e != 0 : 종속
- 유의확률이 0.05보다 크면 귀무가설이 채택된다
가설 검정
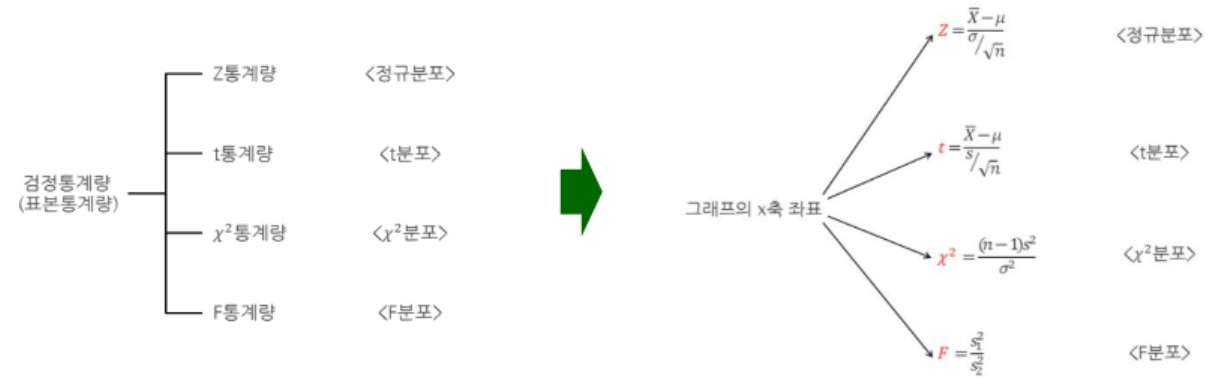
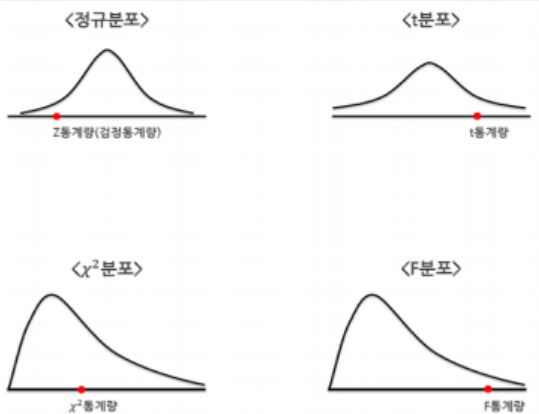
- 가설검정은
모집단의 모수가 이럴 것이다라를 가설을 위해 모수인 u, a^2, p를 사용해서 귀무가설과 대립가설 설정- 일반적으로 표본통계량으로 대체
- 각 표본집단에 맞는 확률분포에 따라 신뢰구간 추정
- 각 확률분포의 x 값을 검정통계량으로 사용
t분포; t-distribution
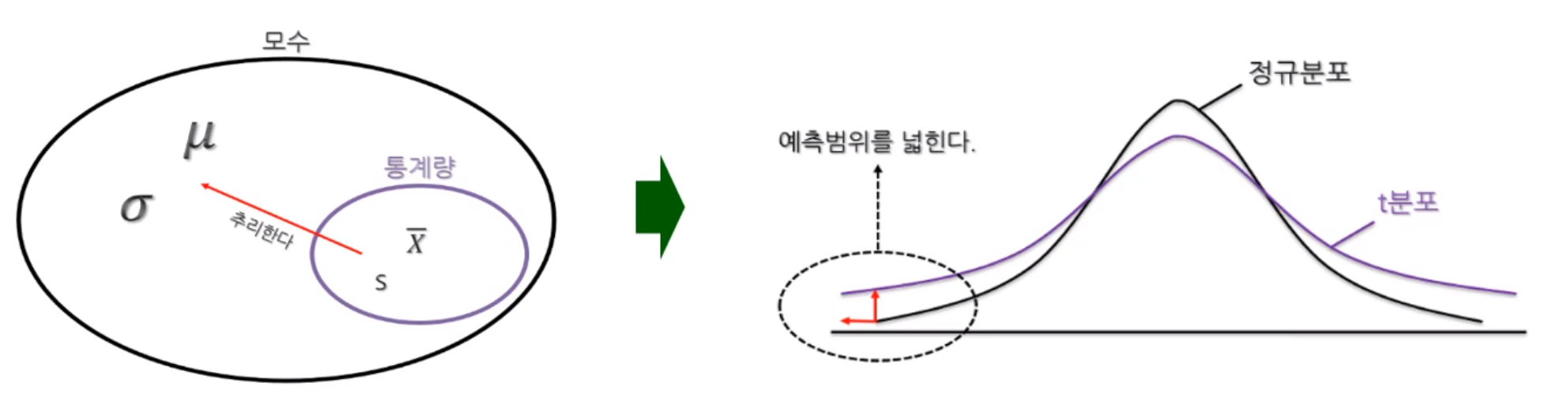
- 모집단의 특징을 분석하기에는 시간과 비용의 제약으로 일반적으로 표본조사를 실시하고, 이를 모집단과 같을 것임을 추정함
- 표본의 개수가 적으면(일반적으로 30개 미만) 신뢰도가 낮아짐
- 따라서 정규분포 보다 예측 범위가 넓은 분포인 t-분포를 사용
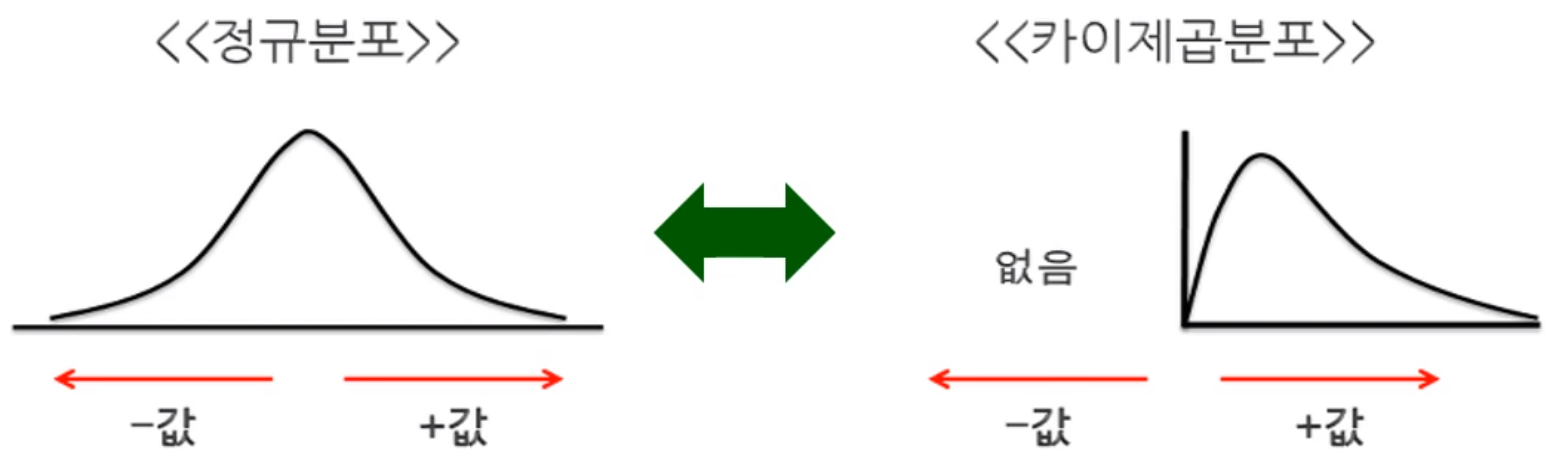
카이제곱 분포
- 명목 및 서열척도의 범주형 변수를 분석하기 위해 한 변수의 범주를 다른 변수의 범주에 따라 빈도를 교차분석하여 두 변수 간 독립성과 관련성을 분석
- 제곱된 값 분산을 다루기 때문에 음수값이 없고 양수만 존재 - 오른쪽 만 꼬리가 긴 비대칭 모양
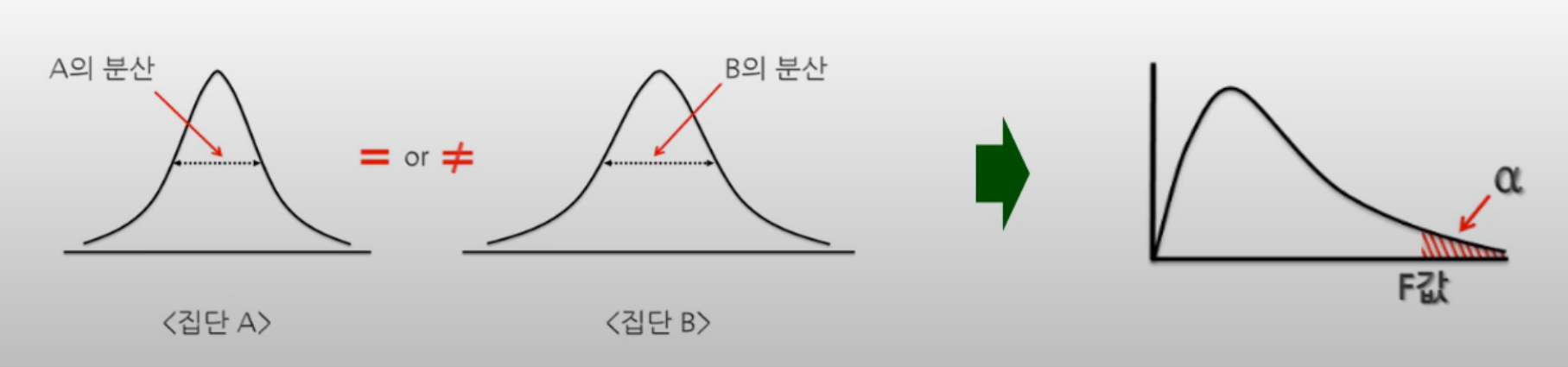
F분포; F-distribution
- 집단의 분산을 추정하고 검정할 때 사용하는 분포
- 카이제곱 분포와 유사하나 한 집단의 분산을 파악하는 카이제곱과 달리 F분포는 두 집단의 분산을 비교
- 3개 이상 집단의 분산을 비교하는 것을 보통 분산분석:Analysis of Variance이라고 하며 신뢰구간 추정과 가설검증, 분산분석에 F-분포가 많이 사용됨
요인분석
- 일련의 관측된 변수에 근거하여 직접 관측할 수 없는 요인을 확인하는 분석 기법
- 경제활동, 가계수입, 주택보급율, 출생률 등 수많은 변수를 사용해야 하나, 몇가지 적은 변수로 묶어 단순화하는 것
- 항목 간의 상관관계가 높은 것끼리 하나의 요인으로 묶거나 중요도가 낮은 변수는 제거
- 하나의 요인으로 묶어진 항목들은 하나의 개념을 측정한 것으로 간주하며, 요인 내의 항목은 수렴적 타당성, 요인간에는 변별적 타당성이 적용된 것으로 해석
- 같은 개념을 측정하려고 하는 변수들이 동일한 요인으로 묶이는지 확인하고자 하는 경우
- 전제조건
- 모든 변수가 드간척도 이상의 연속형 변수로 측정되어야 함
- 각 변수는 서로 독립이며 정규분포, 등분산을 이루고 있어야 함
- 표분의 수는 50이상 내지 변수의 5배수 이상을 권고하고 있음