
정규분포의 예시
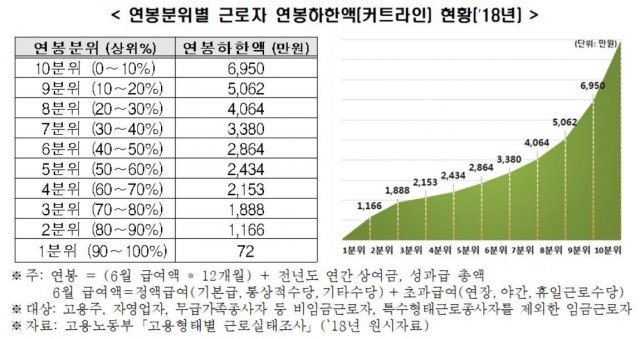
정규분포 Normal Distribution
- 연속확률변수에 속하고 모분포, 가우스 분포라 하여 이상적인 모형
- 평균 : 모집단평균
- 분산 : <b선모집단분산
- 평균과 표준편차에 의해 정의되고 결정되는 대칭 곡선
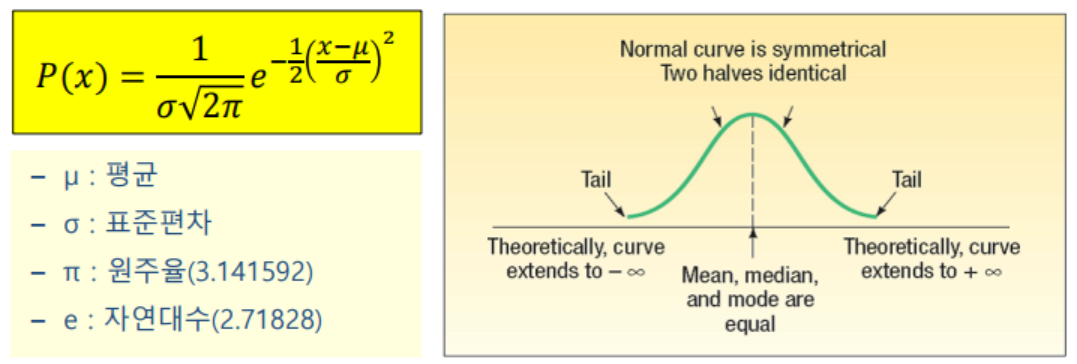
- 평균 = 중앙값 = 최반값
- 분포의 곡선 면적은 1.00
- 평균에 대해서 대칭형태
- 확률 값은 중앙값에 양 극단으로 갈수록 0에 가까워짐(무한대)
- 평균값에 의해 결정되고, 분포는 표준편차에 의해 결정
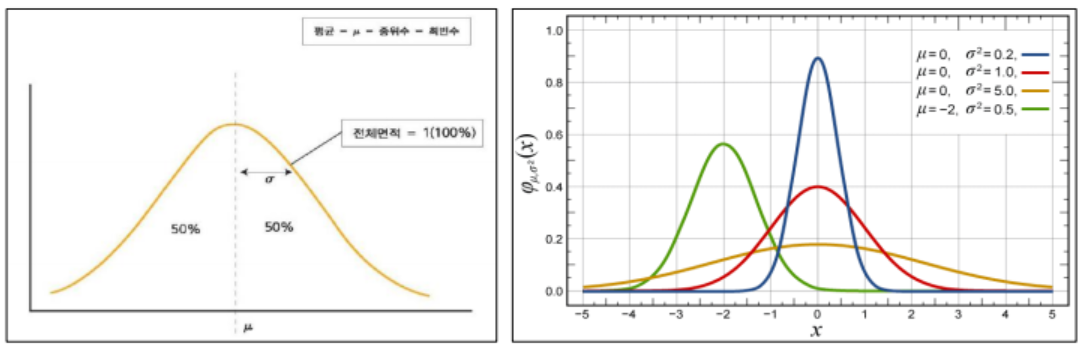
표준정규분포 : z-분포
- 평균=0, 표준편차=1 인 정규분포를 표준정규분포라고 함

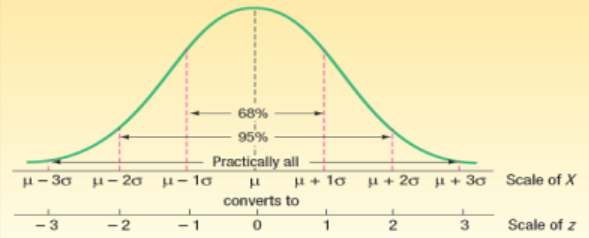
- 표준정규확률분포(z값)
- 확률분포표는 양수 z의 값에 대해서 표준정규분포가 0~z사이에 있을 확률(면적)을 기록한 것
- 음영표시 확률 (47.5%)는 z값 1.9와 0.06을 합쳐 1.96이며, 절대값 1.96 바깥에 있는 부분의 확률은 2*0.025=0.05 , 즉 5%
- 이는 표준편차 1.96배 바깥의 범위의 확률이 5%라는 의미
중심극한정리 central limit theorem
- 정규분포를 이루는 모집단에서 추출한 표본집단의 평균과 표본분포는 정규분포를 갖음
- 모집단이 정규분포가 아니라도 표본의 크기가 증가함에 따라 모집단에 관계없이 표본집단 평균은 정규분포에 가까워지는데 이를 중심극한정리라 함
- 대상자가 30명 이상 일 때, 모집단에 상관없이 표본집단은 정규분포를 이룬다고 하고, 대상자수가 많을수록 정규성에 가까워짐
문제풀기 1
문) 전문뉴스 라디오채널 A방송 청취자의 평균 청취시간 분포가 정규분포를 따른다고 가정할 때, 이 분포의 평균은 15.0분, 표준편차는 3.5분이다.
각 구간별 청취시간을 나타낼 확률을 구하시오
- 20분 이상
- 20분 이하
- 10분과 12분 사이
- 25분 이상
- Tip : NORM.DIST(x,y,z, True) 활용
- 20분 이상
1 | =norm.dist(20, 15.0, 3.5, true) |
20분 이상 청취할 확률은 1.0 - 0.9234 = 0.0766 -> 7.6%
문제풀기 2
문) 우리집 막내A 는 중학교 2학년에 재학중이다. 이번 중간고사 시험결과가 학교로부터 우편으로 배달되었다. 시험결과 안내는 A의 등수가 아니라 표로 제시되었다.
| A의평균점수 | 2학년 평균점수 | 2학년 표준편차 | 2학년 학생 수 |
|---|---|---|---|
| 81.5 | 78.6 | 16.4 | 347 |
- 2학년 전체의 시험성적이 정규분포를 나타낼때 A의 등수는?

