
변수의 종류
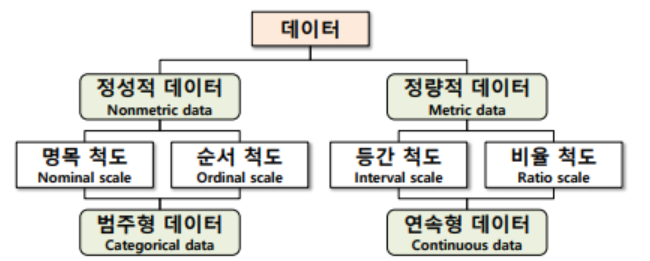
척도에 따른 분류
- 척도 : 입력자료를 수치적으로 측정하는 단위
- 명목 척도 : 성별, 직업, 지역 -> 순서와 무관, 수학적 계산 불가
- 순서 척도 : 대소, 다과 등 서열적 자료 -> 순서상 상대적 위치 표현
- 등간 척도 : 온도, 만족도 -> 수학적 연산 가능
- 비율 척도 : 매출액, 가격 -> 절대적 원점 존재, 수학적 연산 가능
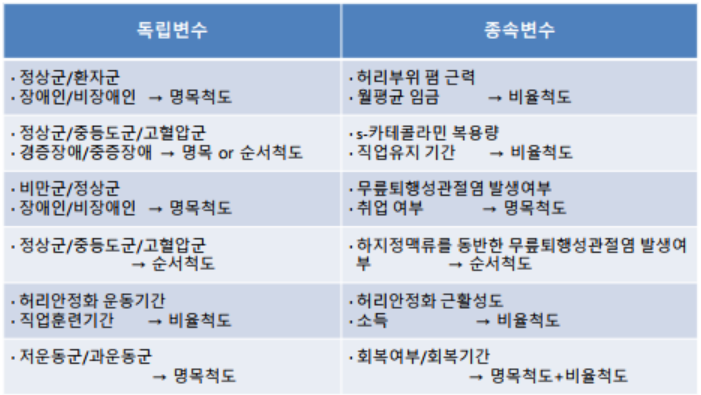
인과관계예 따른 분류
- 독립변수(설명변수)
- 다른 변수에 영향을 주는 변수
- 원인에 해당
- 종속변수(반응변수)
- 다른 변수에 영향을 받는 변수
- 결과에 해당
자료형식에 따른 분류
- 숫자변수
- 숫자로 처리되는 변수
- 문자변수
- 문자열로 처리되는 변수
- 날씨변수
- 날짜 표기형식으로 처리되는 변수
기술통계와 추론통계
- 기술통계
- 측정이나 실험으로 수집한 자료의 정리, 표현, 요약, 해석 등을 통해 자료의 특성과 변수 간의 관계를 분석하는 통계적 방법
- 도수분포, 백분율, 평균, 표준편차 등 분석 포함
- 추론통계
- 표본정보를 가지고 그 모집단의 특성 및 가능성 등을 추론해내는 통계적 방법
- 표본통계량을 이용하여 모수를 추론
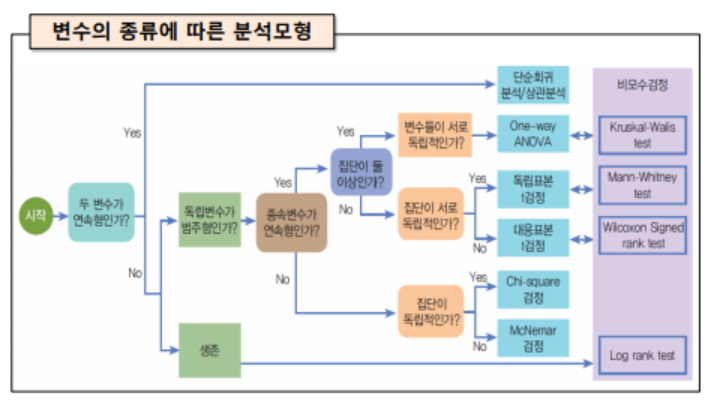
- 추론과정에서 모집단의 분포가 정규분포이면 모수검정 실시
- 모집단이 정규분포를 가정하지 못하면 비모수검정 실시
범주형 데이터 기초분석
- 빈도분석
- 실행메뉴
- 분석 -> 기술통계량 -> 빈도분석
- 분석할 변수의 빈도, 퍼센트, 무응답을 제외한 유효퍼센트, 누적퍼센트 등이 분석
- 실행메뉴
- 통계량
- 수학적 분석결과 표시
- 백분위수
- 산포도
- 중심경향
- 분포
- 도표
- 범주형 변수
- 막대도표
- 원도표
- 정량적 변수
- 히스토그램
- steam&leaf
- Box-plot
- 범주형 변수
연속형 데이터 기초 분석
기술 통계값
- 주어진 데이터를 요약하며 의미 있는 몇 개의 값으로 분석
- 요약과정에서 정보의 손실에 의한 정확성이 상실되나, 대부분 요약성이 정확성보다 중요한 의미를 갖음
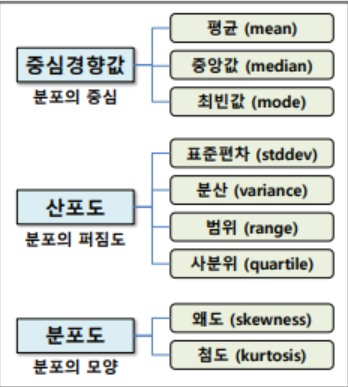
평균값 mean
- AVERAGE()
- 평균값은 어디에나 존재
- 자료의 모든 값을 고려
- 극단치에서 변동의 폭이 심함

중앙값 median
- MEDIAN()
- 중앙값은 어떤 경우에나 존재
- 자료의 모든 값 자체를 고려하지는 않고 몇 개의 값이 있는지만 고려
- 극단적인 자료에서도 크게 변하지 않음
- 극단치가 있다면, 평균값보다 중앙값이 더 대표성을 띔
최빈값 mode
- MODE()
- 특히 이름으로 표현한는 명목변수나 이산변수를 기술할 때 사용
- 하나 이상일 수 있지만, 전혀 없을 때도 있음
- 모든 값을 반영하지는 않음
범위 range
- MAX() - MIN()
- 연속형 변수에서 사용
- 변수의 최고값에서 최소값을 뺀 것
- 계산하기에 간편함
- 최고값과 최소값에 의해서 범위가 결정되므로 그 사이에 값들의 퍼진 정도는 알수 없음
- 극단치가 있을 때는 변동이 큼
분산 variance
- 모집단의 분산 VAR.P()
- 표본집단의 분산 VAR.S()
- 측정값의 편차를 제곱하여 계산
- 모 분산의 단위는 관측 값이 갖는 측정단위와 일치하지 않음
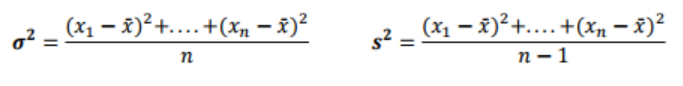
표준편차 standard eviation
- 모집단 표준편차 STDEV.P()
- 표본집단의 표준편차 STDEV.S()
- 분산의 양의 제곱근
- 측정값의 측정단위와 일치하기 위함
- 크다
- 자료가 평균값을 중심으로 광범위하게 분포
- 작다
- 평균값을 중심으로 밀접하게 분포
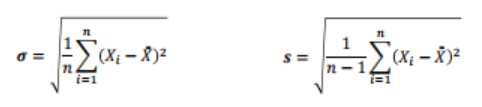
- 평균값을 중심으로 밀접하게 분포
변동계수 coefficient of variation, CV%
- 변동계수는 표준편차를 평균으로 나눈 값
- 측정단위에 따라 표준편차의 값의 크기가 달라지므로, 단위가 다른 두 집단을 비교하는 경우, 두 표준편차의 단위를 같게 하기 위해 표준편차를 평균으로 나눈 값에 100을 곱하여 CV%로 표시(그전에는 단위가 없음)
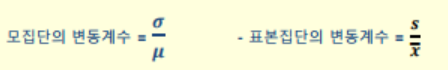
사분위수범위 interquartile range : IQR
- 상위 25%에 해당하는 값과 하위 25%에 해당하는 값을 제외하고 범위를 구한 값
- IQR는 주우이수를 중심으로 상위25%와 하위 25% 관측값의 차이를 의미

왜도 skewness
- SKEW()
- 0SKEW.P()
- 분포도의 기울어진 방향과 정도를 나타내는 양
- '0’에 가까울수록 정규분포와 비슷


첨도 kurtosis
- KURT()
- 분포도의 모양이 얼마나 뾰족한 가를 나타내는 양
- '0’에 가까울수록 정규분포와 비슷

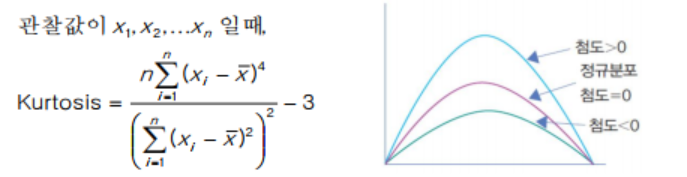
엑셀에서 통계도구 사용하기
- 파일 -> 옵션 -> 추가기능 -> 분석도구 -> 이동 -> 분석도구 check
- 데이터 탭 -> 데이터분석